Trigonometria

A Trigonometria (trigono: triângulo e metria: medidas) é o estudo da Matemática responsável pela relação existente entre os lados e os ângulos de um triângulo. Nos triângulos retângulos (possuem um ângulo de 90º), as relações constituem os chamados ângulos notáveis, 30º, 45º e 60º, que possuem valores constantes representados pelas relações seno, cosseno e tangente. Nos triângulos que não possuem ângulo reto, as condições são Dois triângulos são ditos semelhantes se um pode ser obtido pela expansão uniforme do outro. Este é o caso se, e somente se, seus ângulos correspondentes são iguais. O fato crucial sobre triângulos semelhantes é que os comprimentos de seus lados são proporcionais. Isto é, se o maior lado de um triângulo é duas vezes maior que o lado do triângulo similar, então o menor lado será também duas vezes maior que o menor lado do outro triângulo, e o comprimento do lado médio será duas vezes o valor do lado correspondente do outro triângulo. Assim, a razão do maior lado e menor lado do primeiro triângulo será a mesma razão do maior lado e o menor lado do outro triângulo.

Usando estes fatos, definem-se as funções trigonométricas, começando pelos triângulos retângulos (triângulos com um ângulo reto 90 graus ou π/2 radianos). O maior lado em um triângulo qualquer é sempre o lado oposto ao maior ângulo e devido a soma dos ângulos de um triângulo ser 180 graus ou π radianos, o maior ângulo em um triângulo retângulo é o ângulo reto. O maior lado nesse triângulo, consequentemente, é o lado oposto ao ângulo reto, chamado de hipotenusa e os demais lados são chamados de catetos.

Dois triângulos retângulos que compartilham um segundo ângulo A são necessariamente similares, e a proporção (ou razão) entre o comprimento do lado oposto a A e o comprimento da hipotenusa será, portanto, a mesma nos dois triângulos. Este valor será um número entre 0 e 1 que depende apenas de A. Este número é chamado de seno3 de A e é escrito como \operatorname{sen}(A). Similarmente, pode-se definir :

o cosseno (ou co-seno) de A: é a proporção do comprimento do cateto adjacente ao ângulo A em relação ao comprimento da hipotenusa

a tangente trigonométrica de A: é a proporção do comprimento do cateto oposto ao ângulo A em relação ao comprimento do cateto adjacente

a co-tangente de A: é a proporção do comprimento do cateto adjacente ao ângulo A em relação ao comprimento do cateto oposto - é o inverso da tangente

a secante trigonométrica de A: é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto adjacente ao ângulo A - é o inverso do cosseno

a co-secante de A: é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto oposto ao ângulo A - é o inverso do seno.adaptadas na busca pela relação entre os ângulos e os lados.

A trigonometria possui inúmeras aplicações nos diversos ramos da ciência, sendo considerada uma importante aliada do mundo moderno.
Observe os exemplos a seguir:

Exemplo 1 Ao decolar, um avião sobe formando um ângulo de 30º com a pista (horizontal). Na direção do percurso existe uma torre de transmissão de energia elétrica situada a 3km do aeroporto e com altura igual a 150 metros. Verifique se, mantendo o trajeto, o avião pode colidir com a torre.

Esquema da situação:

Usaremos a relação da tangente

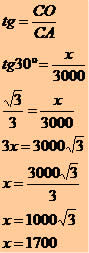
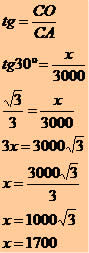
O avião não irá colidir com a torre, pois essa possui 150 metros enquanto o avião estará a uma altura de 1700 metros.

Exemplo 2 
Do ponto A, uma pessoa observa o topo de uma torre sob um ângulo de 60º. Determine a altura da torre, sabendo que a pessoa está a 20 metros dela.

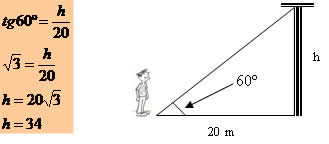
A torre tem 34 metros de altura.

Exemplo 3
Uma inclinação tem 40 metros de comprimento e forma com o plano horizontal um ângulo de 30º. A que altura está situado o ponto mais alto da inclinação?

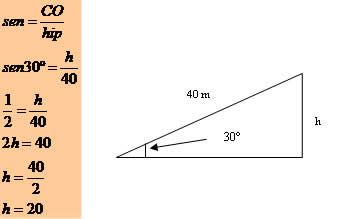
Créditos: Mundo educação.